Questão 1
Dadas as matrizes  ,
,  e
e  , determine a matriz D resultante da operação A + B – C.
, determine a matriz D resultante da operação A + B – C.
 ,
,  e
e  , determine a matriz D resultante da operação A + B – C.
, determine a matriz D resultante da operação A + B – C.
Questão 2
Os elementos de uma matriz M quadrada de ordem 3 x 3 são dados por aij, onde:
i + j, se i ≠ j
0, se i = j
Determine M + M.
i + j, se i ≠ j
0, se i = j
Determine M + M.
Questão 3
(PUC–SP–Adaptada) São dadas as matrizes A = (aij) e B = (bij), quadradas de ordem 2, com aij = 3i + 4j e bij = – 4i – 3j. Considerando C = A + B, calcule a matriz C.
- Questão 4(PUCC–SP–Adaptada) Seja a matriz A = ( aij ) 2 x 2, em que aij = i + j, se i = j e i – j, se i ≠ j. Determine a matriz respeitando essas condições e calcule A + A + A.
- Questão 5Determine a matriz C, resultado da soma das matrizes A e B.

- Questão 6Adicione as matrizes e determine os valores das incógnitas.

- Questão 7Determine a matriz resultante da subtração das seguintes matrizes:
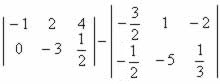
- Questão 8Considerando as matrizes:

Determine:
a) A + B – C
b) A – B – C
Respostas
- Resposta Questão 1
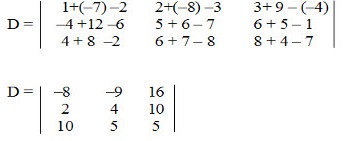
- Resposta Questão 2

- Resposta Questão 3

- Resposta Questão 4
.jpg)
- Resposta Questão 5
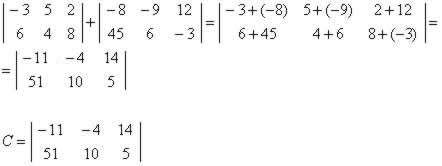
- Resposta Questão 6
x + x = 10
2x = 10
x = 5
y + 3 = – 1
y = – 1 – 3
y = – 4
3 + t = 4
t = 4 – 3
t = 1
2z + z = 18
3z = 18
z = 18/3
z = 6 - Resposta Questão 7
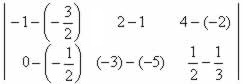

- Resposta Questão 8

- Questão 1UFSC
Sejam A=(aij )4x3 e B=(bij )3x4 duas matrizes definidas por aij=i+j e bij=2i+j, respectivamente. Se A.B=C, então qual é o elemento c32 da matriz C?
- Questão 2Encontre o valor de x e y resolvendo a seguinte igualdade.
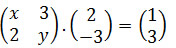
- Questão 3Determine os valores de a e b para que as matrizes sejam comutativas.
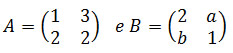
- Questão 4FGV-SP (questão adaptada)
 , de forma que At.B é uma matriz nula, calcule x.y2
, de forma que At.B é uma matriz nula, calcule x.y2 - Questão 5(Fuvest-SP)
Uma matriz real A é ortogonal se A.At=I, onde I indica a matriz identidade e Atindica a transposta de A.
a) 1/4
b) √3/4
c) 1/2
d) √3/2
e) 3/2
Respostas
- Resposta Questão 1
O elemento requerido é o da terceira linha e da segunda coluna, que é resultado de uma multiplicação de duas matrizes. Sabemos pela propriedade de multiplicação que este elemento é proveniente da multiplicação da terceira linha da matriz A pela segunda coluna da matriz B. Portanto, precisamos escrever apenas estes elementos.

- Resposta Questão 2
Ao resolvermos a multiplicação do lado esquerdo da igualdade, obteremos uma matriz-produto, de forma que poderemos igualar a matriz-produto à matriz do lado direito da igualdade.

- Resposta Questão 3
A propriedade da comutatividade diz que dois elementos são comutativos quando a seguinte igualdade é verdadeira: A.B = B.A.
Façamos isto com nossas matrizes:

Basta obtermos o produto de cada lado da igualdade:

Igualando os dois produtos:

Não é preciso fazer a igualdade de todos os elementos, basta escolhermos os elementos que possuem apenas um dos valores, para facilitar os cálculos:

- Resposta Questão 4
Temos que encontrar a matriz transposta de A.

Temos que
Resolvendo a multiplicação das matrizes, temos:

A questão pede o valor de x.y², agora que obtemos o valor de cada um podemos resolver essa expressão.

- Resposta Questão 5
Devemos primeiramente calcular o produto da matriz A pela sua matriz transposta, igualando-as à matriz identidade.

Como a matriz é ortogonal, temos que A.AT=I.
Com isso,

Com estas informações podemos montar um sistema através da igualdade de matrizes.

Da primeira equação obtemos que o valor de x é igual a:

Substituindo este valor na segunda equação obtemos uma expressão para z.

Substituindo na terceira equação o valor de z, temos:

A questão pede o valor de x²+y². Como sabemos o valor de cada um, é possível calcular este resultado:

Resposta letra E
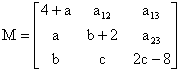
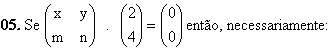
A 4º questão a virgula está errada façam o favor de corrigi-la o certo seria : Seja A=(aij) se I=J, e i-J se ifor diferente de J
ResponderExcluirdesnecesário
ResponderExcluirEste comentário foi removido pelo autor.
ResponderExcluirE muito ruim não achei a minha resposta ruimmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmm
ResponderExcluirÉ muito bom achei as minhas respostas
Excluir